There are a lot of great resources for learning French online. Out of the many that I have visited, one of my favorites is a website called Français Facile. The name translates to "Easy French" and contains a plethora of material for learning the French language. Notably, there are over 1600 learning exercises on the site. Personally, I find these exercises exteremely useful to ameliorate my understanding of French grammar. Therefore, I've decided to archive the exercises for my personal use. This article is an outline of the process I used to generate this archival.

Basics of the site

From first impressions, Français Facile appears to be an older site. The design of the website is archaic relative to modern day design. The site uses HTML and some JS for rendering content on the website. Additionally, the site runs PHP for generating page content and other tasks.

Finding all of the exercises

My first goal was to gain a good understanding of the site's organizatin of pages/routes. If I wanted to archive all the exercises on the site, I needed to first learn the total count of exercises and their URLs. Ideally, there would be an API which would let me query for a list of all exercises. After some preliminary research, I was not able to find any public API endpoints on the francaisfacile.com domain. Therefore, I had to turn to web scraping.

The url francais.facile.com/exercices returns which can be used to begin browsing exercises on the site. Immediately I noticed the following form:

This form allows you to browse exercises by type. There are several different options in the dropdown. However, one of the options is thankfully Tous les exercices or All exercises. Submiting this option, redirects the user to the following page:

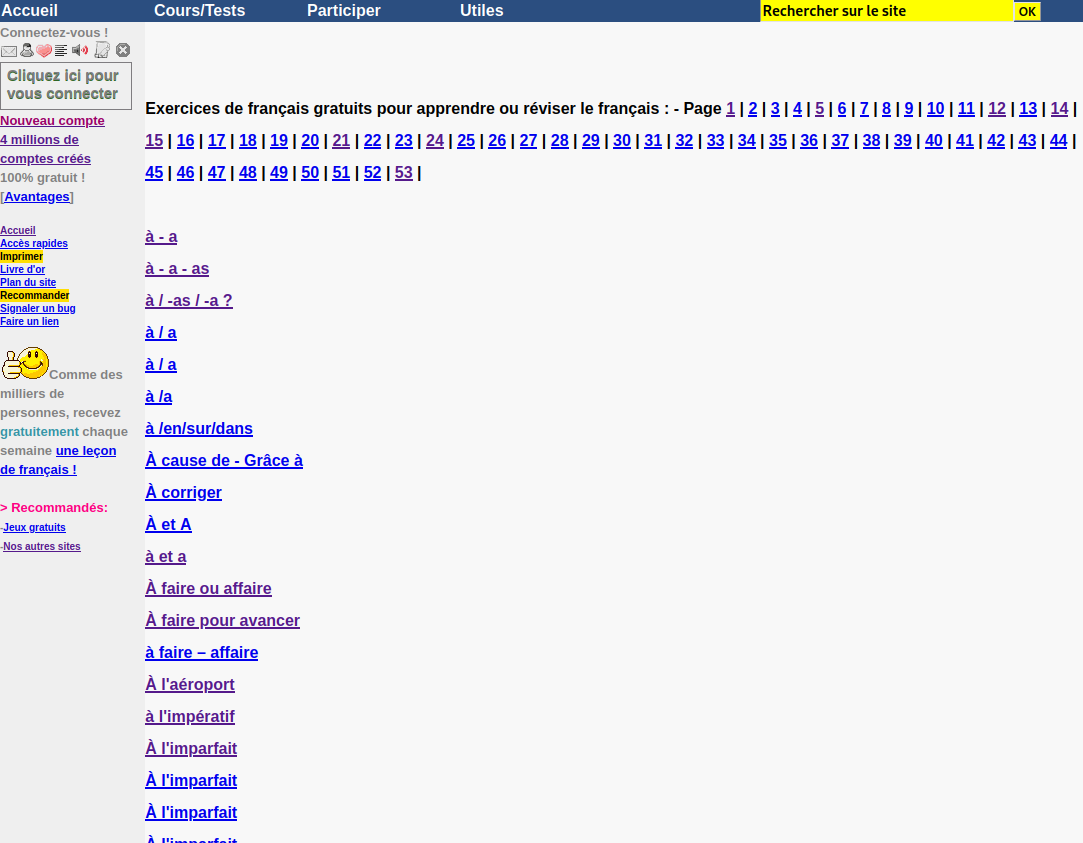
This single page contains links to 200 separate exercises. By looking at the top, we can see that exercises are paginated into 53 seperate pages. The url for each page follows the format of https://www.francaisfacile.com/free/exercices/exercices-francais-{PAGE_NUMBER}.php. Therefore, we can iteratively go through each of the 53 pages and extract links for each of the exercies present. So far, this is the best method I've found to construct a list of all exercises.

To get all of the links for each available exercise, I wrote a simple Python script. I used requests to retrieve the pages HTML content and BeautifulSoup4 for parsing the HTML. Here are my imports:

import re
import requests
from bs4 import BeautifulSoup


exercise_pattern = re.compile(r'\/cgi2\/myexam\/voir2\.php\?id=\d+')

Presumablly, more pages of exercises could be added in the future, so I created a function that would return URLs for each page of exercises:

def page_links() -> list[str]:
    '''
    Retrieves the URL for each of the 53 pages which list exercises
    '''
    # Pattern of page URLs mentioned above
    page_pattern = re.compile(r'https\:\/\/www\.francaisfacile\.com\/free\/exercices\/exercices-francais-\d+\.php')
    first_page = 'https://www.francaisfacile.com/free/exercices/exercices-francais-1.php'
    text = requests.get(first_page).text
    soup = BeautifulSoup(text, features='html.parser')
    links = [node.attrs['href'] for node in soup.find_all('a', { 'href': page_pattern })]
    # remove duplicates just in case
    non_duplicate_links = list(set(links))
    return non_duplicate_links

The page_links() function returns a list of URLs for each page. It's then possible to iteratively go through the list of each URL, fetch the HTML, and parse the markup for every exercise page URL. I do this in the following function:

def exercise_links_on_page(list_page: str) -> list[str]:
    '''
    Get links for every exercise on a single page. Returns a list of exercise URLS.

    arguments:
    list_page: str -- The URL for the page to scrape exercise URLs from.
    '''
    text = requests.get(list_page).text
    soup = BeautifulSoup(text, features='html.parser')
    soup = soup.find('main')
    links = [node.attrs['href'] for node in soup.find_all('a', { 'href': exercise_pattern })]
    return links

Fetching HTML for all exercises

From the functions page_links and exercise_links_on_page, I know had a list of URLS for over 1600 exercises. To the best of my knowledge, this is the most exhaustive list of exercises I could obtain. From this list, I began to fetch the HTML for each of the 1600 pages.

Since this is a free website and I wanted to be respectful, I severely rate limited each of the 1600 HTTP requests. I created a simple function that iteratively went through each exercise URL and made an HTTP GET request.

# Pseudocode for fetching the HTML for each exercise
for url in exercise_urls:
    # Each URL has the exercises internal ID
    exercise_id = get_id_from_url_substring(url)
    response = make_http_get_request(url)
    HTML = response.body
    save_to_disk('./exercises/{id}.html', HTML)

I decided to save the HTML to disk for each exercise. This way I could avoid making additional HTTP requests while I debug.

After completing all 1600+ HTTP requests and saving their results to disk, I now had access to all of the exercises for parsing and archival. Additionally, each file contains the exercise ID within the file name. This ID serves served as a good index for persisting the data into a database.

Parsing each exercise

Creating a script to accurately parse each exercise was the most difficult part of the process. There are several reasons why this was the case.

Fundamentally, HTML is not a semantic markup language. It's hard to seperate data from the markup because there is not always a clear indication of the data's location.

Additionally, browsers do not enforce HTML conventions. Browsers will even render HTML that is incomplete. Therefore, when trying to parse HTML, you are at the mercy of the person who wrote it. There are no guarantees that the HTML is syntatically correct.

Unfortunately, the HTML used by Français Facile is a mess. Elements are not nested logically and the use of semantic IDs or classes is sparse. I had to make as few assumptions as possible when parsing each exercise. This resulted in me writing conditional logic for certain types of exercises so they could be parsed accurately.

From my preliminary research, I discovered that there were 6 (technically 7) formats of exercises utilized by the site. Each of these formats required tailor-made algorithms for parsing. Below is a list and a brief description of each format:

Multiple Choice

An exercise that contains multiple choice questions.

Fill in the blank

Contains multiple text boxes that allow users to enter their answers.

Scrambled Words

Each question consists of a list of words in scrambled order. A user must rearrange them to their correct order.

Scrambled Letters

Similar to scrambled words. However, each question contains scrambled letters that must be rearranged to form a word.

Find the Errors

Presents the user a long text. The user must read the text and click on the words that are not gramatical or spelled correctly.

Ordered List

A list of words stacked on top of each other in a list. The user must rearrange this list to match the given criteria.

Custom Java Applet

The site contains some exercises that were written as Java Applets. However, Java for the web is long extinct. Since there were only a few of these questions, I decided not to parse them.

Parsing strategies

Multiple Choice

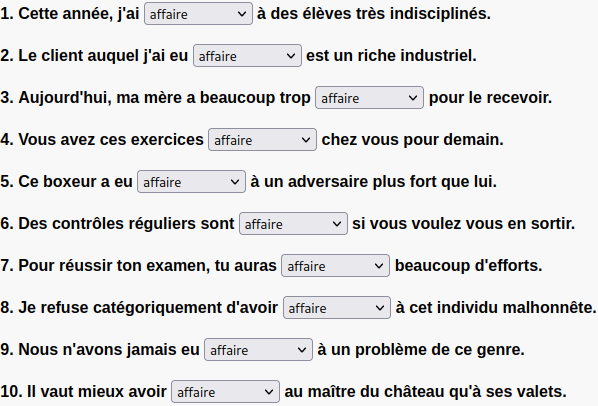
The following is an example of the DOM for one multiple choice question:

1. Cette année, j'ai
<select name="p1">
  <option value="affaire">affaire</option>
  <option value="à faire">à faire</option>
  <option value="" style="color:grey;">Je ne sais pas</option>
</select>
à des élèves très indisciplinés.
<br />
<br />
<input type="hidden" name="r1" value="affaire" />
<input
  type="hidden"
  name="q1"
  value="Cette année, j'ai * à des élèves très indisciplinés."
/>

Luckily, all of the <select> tags had a name attribute which contained the question number prefixed by a p. It was simple to query the DOM for all of the <select> tags. Using BeautifulSoup, it looked something like this:

soup.find_all('select', { 'name': re.compile(r'^p\d+$') })

This query allowed me easily to fetch the multiple choice options for each question.

Next, I had to retrieve the prompt and answer for each questions. Conveniently, when looking at the DOM, each question is followed by two <input> elements that are not rendered. The first of these <input> tags contains a value attribute which contains the correct answer for the question. I only had to extract that attribute value to fetch the answer for each question.

The second hidden <input> element contains a value attribute. This value attribute contains the question prompt with a * placeholder.

Parsing the <input> and <select> tags for each multiple choice exercise allowed me to receive all the necessary data to recreate these exercises.

Fill in the blanks

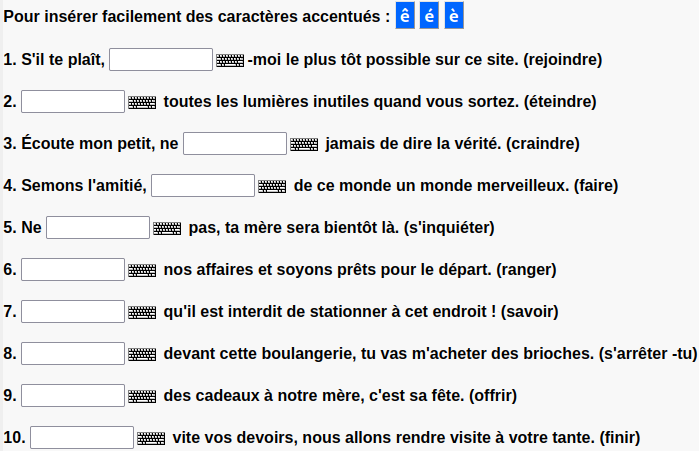
The format of fill in the blank exercises is straightforward. Each question has a <input> tag where the user can enter in their answer. Below is an example of the DOM for one question.

1. S'il te plaît,
<input
  type="TEXT"
  size="10"
  class="keyboardInput"
  maxlength="10"
  name="p1"
  onfocus="active('1')"
  onkeyup="deuxespaces('1')"
  vki_attached="true"
  _scrolltop="0"
/>
<img
  src="/cgi2/myexam/mykey.png"
  alt="Display virtual keyboard interface"
  class="keyboardInputInitiator"
  title="Display virtual keyboard interface"
  width="28"
  height="13"
/>
-moi le plus tôt possible sur ce site. (rejoindre)
<br /><br />
<input type="hidden" name="r1" value="rejoins" />
<input
  type="hidden"
  name="q1"
  value="S'il te plaît, *-moi le plus tôt possible sur ce site. (rejoindre)"
/>

Just like the multiple choice exercises, there was two hidden <input> elements that contained the question's prompt and answer in the value attribute.

Scrambled Words and Letters

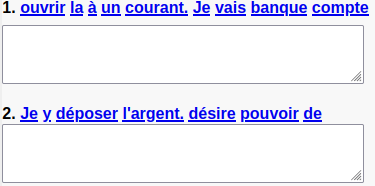
Scrambled word exercsises consist of a <textarea> with muliple <div> siblings. Below is an example of a question:

<div id="cannotid1">word #1</div>
<div id="cannotid2"></div>
<div id="cannotid3" />
<div id="cannotid{N}" />
<textarea />
<input type="hidden" name="r1" value="answer #1" />
<br />
<br />
<div id="cannotid{N+1}">word #N+1</div>
<div id="cannotid{N+2}">word #N+2</div>
<div id="cannotid{N+3}">word #N+3</div>
<textarea />
<input type="hidden" name="r2" value="answer #2" />

Each <div> that contains an id attribute which contains cannotid contains one of the scrambled words/letters. Parse all of the scrambled words, it's necessary to extract the text from each one of these <div> tags. However, there is no indication of how many scrambled words that there. Therefore, to receive all of the words/letters for one question, I had to begin my traversal at the very first sibling (<div id="cannotid1">), and sequentially read the text of each div until I encountered a <textarea>. When I encountered a <textarea>, I knew that a new question was beginning.

Like the previous exercise formats, there is a hidden <input> tag which contains pertinent metadata. This hidden tag contains the answer for the question.

Find the errors

<table />
<input
  type="hidden"
  name="touteslesreponses"
  value="#chante#va#recopie#sont#es#avons#êtes#lisent#mangent#échangent"
/>
<input
  type="hidden"
  name="touteslesquestions"
  value="#chantes *#vas *#recopies *#son *#est *#avions *#été *#lise *#mange *#échange *"
/>

Each exercise of this format contains a <table> element which is followed by two hidden <input> tags. The first hidden <input> has a name attribute assigned as touteslesreponses and a value attribute which contains the correct answer of the exercise.

The second hidden <input> tag has a name attribute assigned as touteslesquestions with a value attribute which contains the mispelled/incorrect words.

The assigned values in the value attributes are words delimited by a #. After extracting these values, I only had to split them with the split() method in the str class.

Ordered list

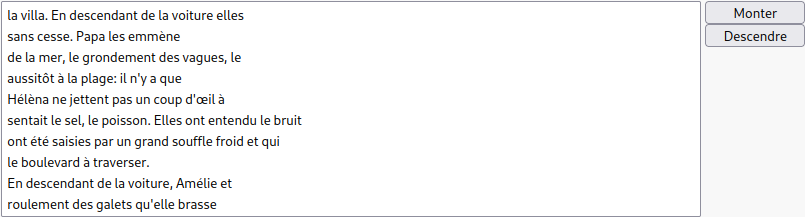
<select name="liste" size="10" style="width:700px">
  <option value="la villa. En descendant de la voiture elles">
    la villa. En descendant de la voiture elles
  </option>
  <option value="sans cesse. Papa les emmène">
    sans cesse. Papa les emmène
  </option>
  <option value="de la mer, le grondement des vagues, le">
    de la mer, le grondement des vagues, le
  </option>
  <option value="aussitôt à la plage: il n'y a que">
    aussitôt à la plage: il n'y a que
  </option>
  <option value="Hélèna ne jettent pas un coup d'œil à">
    Hélèna ne jettent pas un coup d'œil à
  </option>
  <option value="sentait le sel, le poisson. Elles ont entendu le bruit">
    sentait le sel, le poisson. Elles ont entendu le bruit
  </option>
  <option value="ont été saisies par un grand souffle froid et qui">
    ont été saisies par un grand souffle froid et qui
  </option>
  <option value="le boulevard à traverser.">le boulevard à traverser.</option>
  <option value="En descendant de la voiture, Amélie et">
    En descendant de la voiture, Amélie et
  </option>
  <option value="roulement des galets qu'elle brasse">
    roulement des galets qu'elle brasse
  </option>
</select>
<input
  type="hidden"
  name="touteslesreponses"
  value="#En descendant de la voiture, Amélie et#Hélèna ne jettent pas un coup d'œil à#la villa. En descendant de la voiture elles#ont été saisies par un grand souffle froid et qui#sentait le sel, le poisson. Elles ont entendu le bruit#de la mer, le grondement des vagues, le#roulement des galets qu'elle brasse#sans cesse. Papa les emmène#aussitôt à la plage: il n'y a que#le boulevard à traverser."
/>

The ordered list format contains a <select> element with a name attribute which always equals liste. Therefore, a simple BeautifulSoup query like:

soup.find('select', { 'name': 'liste'})

will return the correct <select> tag. Within this tag, there are multiple <option> tags which represent the original order of the question. Just like the previous formats, there is a hidden <input> tag which follows the <select> tag. It's name attribute is assigned the value of touteslesreponses. Within its value attribute is the correct order of question. These terms are also delimited with a #.

Final Results

Originally, I had planned to persist all of the parsed exercise data into a relational database. However, the structure of each exercise is different. For example, for multiple choice questions, it is necessary to parse the availble choices for each question. With fill in the blank type exercises, there are no choices.

Since the data structure of each exercise format is different, I figured that a NoSQL database solution would be more fitting. Specifically, I inserted all of my data as documents in a MongoDB instance. The data was easy to organize into documents. Here is an example of a multple choice exercise document:

// 123 is the exercise id
"123": {
    "type": "multiple_choice",
    "name": "à ou a",
    "choices": ["à", "a", "Je ne sais pas."],
    "correct": "a",
    "prompt": "il * une probleme"
}

I believe this data format will will allow for any necessary type of query. Additionally, having a NoSQL style schema provides flexibility if the site adds or changes exercise formats in the future.

I've been involved in a fair amount of technical interviews lately. I've been asked a plethora of various problems. Most of them are straightforward.

However, I recently encountered the same problem during two separate interviews for two separate companies.

The problem has an interesting solution which I struggled to discover at first. Therefore, I thought it might be valuable for myself and others if I try to outline the problem along with a solution.

The Problem

Given an integer N, determine the largest nondecreasing monotonous integer y where y <= N

Background

The keyword is monotonous. What does a nondecreasing monotonous integer entail?

In mathematics, there exists the monotonic function. Quickly looking at wolfram alpha, we see the following definition:

"A monotonic function ... is either entirely nonincreasing or nondecreasing. A function is monotonic if its first derivative (which need not be continuous) does not change sign."

In other words, if the function f(x) is monotonically nondecreasing, the value f(A) will be always be less than or equal to f(B) if A < B.

Note: A formal explanation can be found on wikipedia.

A simple example of an nondecreasing monotonous function would be f(x) = x or any other linear function with a positive coefficient in front of x.

A nondecreasing monotonous integer follows the same spirit as a nondecreasing monotonic function. The following are examples of such integers:

• 123456789
• 12
• 2
• 1111111
• 02233467
• 3445

Each digit in the integer is less than or equal to its successor. (left to right)

Two Approaches

The Time Inefficient Approach

The simplest and most straightforward approach to this problem would be to write some sort of algorithm that solves through brute force.

For example:

N = 987654321; // Upper bound for solution
solution = 0; // Variable which will hold the solution

for (i = 0; i <= N; i++) {
  // Flag used to mark a possible solution as nondecreasing
  nondecreasing = True
  for (j = 0; j < i - 1; j++) {
    // If the digit at index j is greater than digit at index j + 1,
    // the candidate cannot be nondecreasing
    if (N[j] > N[j + 1]) nondecreasing = False
  }
  // if nondecreasing hasn't been set to false, assign solution to i
  if (nondecreasing) solution = i
}

print "Highest nondecreasing monotonous integer is " + solution

This approach works but it is inefficient.

There are two loops and one is nested within the other. The time complexity of the outer loop is Θ(N). The time complexity of the inner loop is Θ(i).

To extrapolate the time complexity of the entire algorithm, we multiple Θ(N) and Θ(i). This results in Θ(Ni) or roughly Θ(N²) since the upper bound of i increases as N increases.

Ultimately, this approach to the problem is probably not what an interviewer wants to see. Brute force is rarely elegant.

Note: I deliberately use Big-Θ notation instead of Big-O here. This is because both of the loop's time complexities are bounded by N. I feel this is an important distinction when analyzing time complexities of algorithms.

The Time Efficient Approach

First off, it's important to observe that a nondecreasing monotonous integer can be subdivided into integer pairs. The first integer of each pair is less than or equal to the second integer.

For example, here is 1234 subdivided into 3 integer pairs.

(1, 2), (2, 3), (3, 4) <-> 1234

With an integer that doesn't satisfy the requirements of nondecreasing monotonicity, we would get one or more integer pairs where the first integer is greater than the second.

For example, here is 4356 subdivided into 3 integer pairs. Notice that the pair (4, 3) is decreasing.

(4, 3), (3, 5), (5, 6) <-> 4356

In order to transform a non-monotonous integer into a nondecreasing monotonous integer, we must decrement the first integer of every decreasing pair.

This must be done in order from the right most pair to the left most pair. If an integer is decremented, the second value in the next integer pair must be updated to reflect this change.

For 4356, it is only necessary to perform the decrement operation on the first integer pair.

(4, 3) -> (3, 3)

After completing this first step in which decreasing pairs are decremented, we are left with the following integer:

3356 <-> (3, 3), (3, 5), (5, 6)

Now, starting with the integer on the right of the last decremented integer, we assign the remaining integers, moving to the right, to the value of 9

3356 -> 3999

In this example, the first 3 was decremented last. Therefore, starting with the second digit, also 3, we assign each digit to 9. This leaves us with 3999 which is the solution to the problem when N = 4356.

Here is another example that requires multiple decrement operations:

N = 4764

// subdivide into pairs
(4, 7), (7, 6), (6, 4)

// starting from the right, we notice (6, 4) is decreasing
(4, 7), (7, 5), (5, 4) <-> 4754

// then, we notice (7, 5) is decreasing
(4, 6), (6, 5), (5, 4) <-> 4654

// starting with 6, assign remaining values to 9
(4, 6), (6, 9), (9, 9) <-> 4699

When N = 4764, the solution is 4699

Those two steps construct the approach to finding the largest nondecreasing monotonous integer which is less than or equal to N.

Now, let's see it implemented in code. For my implementation, I chose to convert N into an array of ascii codes. This simplifies traversal and mutation of individual digits.

const N = 4764;
// Convert the number into an array of one character strings
const strNumber = `${N}`.split("");
// Get the array of ascii codes
const s = strNumber.map((t) => t.charCodeAt(0));
// Number of digits in N
const n = s.length;

// Marker used to track index of last decremented integer
let marker = n;
// From right to left, check for decreasing pairs
for (let i = n - 1; i > 0; --i) {
  // If true, a decreasing pair was found
  if (s[i] < s[i - 1]) {
    // decrement the first integer in the pair
    --s[i - 1];
    // update marker
    marker = i;
  }
}

// The integer at s[marker] is the integer immediately to the right
// of the last decremented integer. Starting from the marker index,
// assign remaining digits to 9
for (let i = marker; i < n; ++i) {
  s[i] = "9".charCodeAt(0);
}

// Convert the array of ascii codes back to an integer
const largest = +String.fromCharCode(...s);
console.log(`Largest nondecreasing monotonous integer: ${largest}`);

With this algorithm, there are two loops where the majority of operations occur. The first loop has a time complexity of Θ(n) where n is the number of digits in N.

Similarly, the second loop also has a time complexity of Θ(n).

Since the two loops are not nested, we simply add the time complexities of each loop to receive the overall time complexity of this algorithm. The result is Θ(2n) or simply Θ(n).

I doubt there is a solution to this problem which would only require constant time. Therefore, this algorithm is as time efficient as any other optimal solution.

Note: Again, I deliberately used Big-Θ notation here.